
1. 규제 (Regularization)
회귀모델에서의 규제란, 부가정보의 손실을 더해 과대적합 문제를 방지하는 방법이며, 복잡도에 대한 페널티를 유도해 모델 파라미터의 값을 감소시킨다. OLS (Ordinary Least Squares, 최소 제곱 회귀)라고 불리는 회귀모델의 일종이며, 과대적합과 부적합 사이의 균형 조정 파라미터로 볼 수 있다. 주로 유전정보나 텍스트 마이닝 같은 입력 파라미터가 너무 많은 문제에 적용되며, 가장 많은 이용방법은 릿지회귀(Ridge) 와 라쏘회귀(Lasso), 엘라스틱넷(ElasticNet)이 있다. 한편, 규제를 적용했을 때 다음과 같은 효과를 볼 수 있다.
규제의 효과
- 모델 트레이닝 속도가 극단적으로 빠르다.
- 변수 중요도 정보를 제공한다.
- 평가가 극단적으로 빠르다.
- 다양한 문제에서 높은 성능을 보인다.
- 선형 모형이 꼭 필요한 경우가 있다.
2. OLS (Ordinary Least Squared)
규제 모델들에 대해 설명하기 앞서, 먼저 회귀모델이 어떤 의미를 갖는지를 생각해보자. 회귀분석의 과정을 생각해보면, 주어진 데이터로부터 X 값들이 주어지고, 그에 대응하는 예측값 y 를 얻을 수 있다. 하지만, 하나의 선으로 모든 y 값을 정확히 나타낼 수 없기 때문에, 실제 결과와 차이는 존재한다. 이 때의 차이를 잔차라고 부르며, 우리가 원하는 것은 이 잔차(ε)가 최소화되는 편향(β)과 각 변수들의 가중치(α)를 찾는 것이 목표라고 볼 수 있다. 이를 수치로 표현하면 다음과 같다.
이를 측정하는 기준 중 하나인 SSE(Sum of Squared Error) 가 있다. 이는 오차의 제곱값을 합한 결과를 의미하는데, 회귀 모델의 목표는 오차가 최소화 되는 값들을 찾는 것이므로 해당 값이 최소화하는 편향과 각 변수들의 가중치를 찾는다고 봐도 무방하다. SSE 를 수식으로 표현하면 다음과 같다.
그리고 지금부터 설명할 OLS는 오차의 제곱을 최소화하는 편향과 각 변수의 가중치를 추정하는 방식이다. 먼저 단순선형회귀 모델에서 어떻게 편향과 변수 가중치를 추정하는지 살펴보자.
위와 같이 편향과 변수의 가중치를 계산할 수 있고, 같은 원리로 다중선형회귀에서도 계산을 해보자.
3. Ridge 회귀 (Ridge Regression)
그렇다면 첫번째 규제로 언급했던, Ridge 회귀(Ridge Regression) 에 대해서 알아보도록 하자. Ridge 회귀는 단순히 최소 제곱 비용 함수에 가중치의 제곱합을 추가한 모델로, 흔히 L2 규제 라고도 부른다. 수식으로 표현하면 다음과 같다.
위의 수식에서 λ||w||22 부분이 규제항(가중치 벡터의 L2 노름)이며 전개해보면 다음과 같다.
하이퍼 파라미터 λ 를 증가시키면 규제 강도가 증가되고 모델의 가중치 값이 감소한다. 만약 λ = 0 일 경우, Ridge 회귀는 선형회귀와 동일하게 된다. 반면 가중치가 아주 큰 경우 모든 가중치가 거의 0에 가까워지고 결국 데이터의 평균을 지나는 수평선이 된다. Ridge 회귀 비용함수에서 절편에 해당하는 w0 는 규제하지 않는다. 모델의 복잡도와 절편은 관계가 없기 때문이다. 만약 경사하강법에 적용하려면 MSE 그레디언트 벡터에 λw 를 더하면 된다. 아래의 그림을 통해 좀 더 살펴보자.
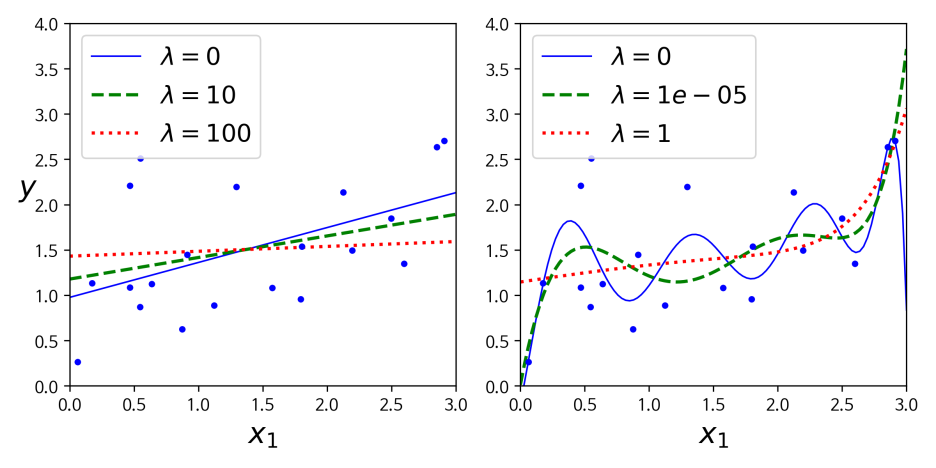
아래의 그래프를 살펴보면 λ 를 증가 시킬 수록 직선에 가까워지는 것을 볼 수 있다.반면 값을 줄이게 되면 모델의 분산은 줄지만 편향이 커지는 현상을 볼 수 있다. 선형 회귀와 마찬가지로 정규방정식을 사용할 수도 있고, 경사하강법을 적용할 수도 있다. 각각의 경우는 아래의 코드로 구현할 수 있다.
import numpy as np
import pandas as pd
from sklearn.linear_model import Ridge, Lasso, ElasticNet, SGDRegressor
from sklearn.model_selection import train_test_split
import statsmodels.api as sm
np.random.seed(42)
data = pd.read_csv("Dataset/housing_data/housing.data.txt", sep="\s+", header=None)
data.columns = ["CRIM", "ZN", "INDUS", "CHAS", "NOX", "RM", "AGE", "DIS", "RAD", "TAX", "PTRATIO", "B", "LSTAT", "MEDV"]
x = data[["LSTAT", "RM", "PTRATIO", "DIS", "NOX", "B", "ZN", "CRIM", "RAD", "TAX"]]
y = data["MEDV"]
# 상수항을 추가합니다.
x = sm.add_constant(x)
# 학습용, 테스트용 데이터 분할
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.3, random_state=42)
# 정규방정식을 적용한 Ridge 회귀
ridge_reg = Ridge(alpha=1, solver="cholesky", random_state=42)
ridge_reg.fit(x_train, y_train)
y_pred = ridge_reg.predict(x_test)library(glmnet)
library(MASS)
# 랜덤 시드 설정
set.seed(42)
# 데이터 읽기
data <- read.table("Data/housing.data.txt", sep="", header=FALSE)
colnames(data) <- c("CRIM", "ZN", "INDUS", "CHAS", "NOX", "RM", "AGE", "DIS", "RAD", "TAX", "PTRATIO", "B", "LSTAT", "MEDV")
# 독립 변수와 종속 변수 분리
x <- data[, c("LSTAT", "RM", "PTRATIO", "DIS", "NOX", "B", "ZN", "CRIM", "RAD", "TAX")]
y <- data$MEDV
# 상수항 추가
x <- cbind(1, x)
# 학습용, 테스트용 데이터 분할
train_indices <- sample(1:nrow(data), size = 0.7 * nrow(data))
x_train <- x[train_indices, ]
y_train <- y[train_indices]
x_test <- x[-train_indices, ]
y_test <- y[-train_indices]
# Ridge 회귀 적용
ridge_reg <- glmnet(as.matrix(x_train), as.matrix(y_train), alpha = 0, lambda = 1)
y_pred <- predict(ridge_reg, newx=as.matrix(x_test))
4. Lasso 회귀 (Lasso Regression)
Lasso 회귀는 Ridge 회귀 처럼 비용 함수에 규제항을 더하지만 L2 노름의 제곱을 2로 나눈 것 대신 가중치 벡터의 L1 노름을 사용한다. 규제 강도에 따라서 어떤 가중치는 0이 될 수 있다. 비용함수는 다음과 같다.
사용된 규제항의 식을 전개하면 아래와 같다.
위의 두 식에 대해 만약 m > n 인 상황이라면 최대 n개의 특성을 선택하는 것이 Lasso 회귀의 한계이다. Lasso 회귀에서의 중요한 특징이 덜 중요한 특성의 가중치를 완전히 제거하려고 하는 것이기 때문이다. 아래 그래프를 통해 좀 더 살펴보자.
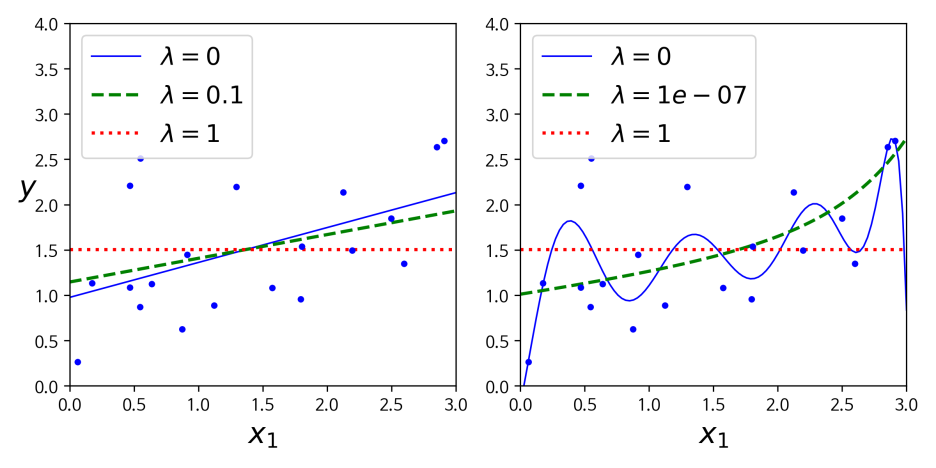
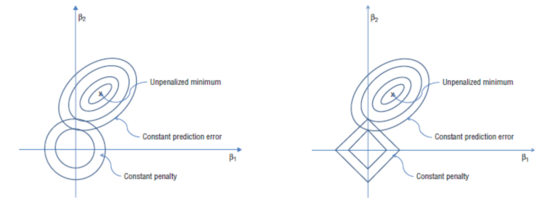
위의 그림은 Ridge회귀와 Lasso 회귀를 오차에 적용했을 때의 모습을 보여준다. 우선 왼쪽이 Ridge, 오른쪽이 Lasso 회귀라는 점을 알아두자. 각 그래프에서 중앙에 위치한 원 혹은 마름모 꼴은 페널티를 의미한다. 또한 그래프 우측 상단에 위치한 타원형은 x,y 의 변화량을 β1, β2 라고 할 경우 (β1,β2) 일 때의 자료에 대한 오차집합체라고 할 수 있다. 일반적으로 Lasso 경우 접점에서 만나기 때문에 자료가 넓게 퍼져있는 것을 선호하며, Ridge의 경우 축 위에서 만나기 때문에 가로축의 값이 0이 되는 것을 선호하는 경향을 보인다.
Ridge의 경우, 만약 동심원이 0이 된다(점이 되는 것)이며 타원형이 갖는 오차 범위가 넓어진다. 타원의 중심이면 최적의 값이자 동심원의 최대 크기지만 학습 자료의 데이터이기 때문에 정확한 값은 아니다.(집합체 안의 일부 값들은 스케일 상 너무 큰 값이 있어서 실제사례로는 적합하지않다.) 따라서 두 원의 접점에 있을 때가 더 적합하다. Lasso의 경우 자료오차 차원이 각 축의 점에 걸린다. 즉, 어느 하나만 크게 하고 나머지는 0으로 준다.
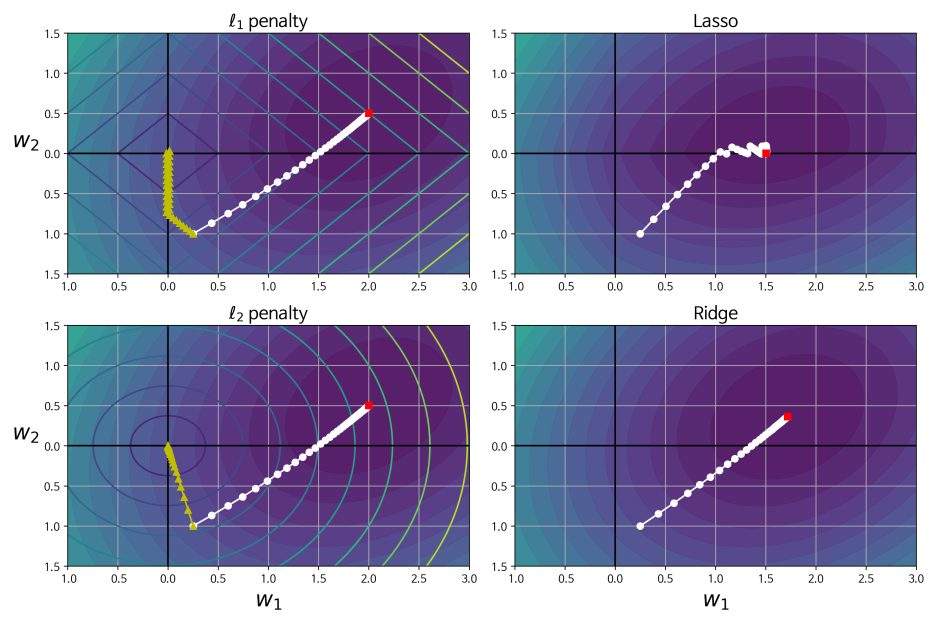
이 그림은 각 회귀모델을 배치 경사하강법을 이용해 그래디언트가 이동하는 경로를 표시한 것이다. 왼쪽 위의 그래프 내 배경의 원형 등고선이 규제가 없는 MSE 함수를 의미한다. 마름모 꼴의 등고선은 L1 페널티를 나타내며, 노란색 삼각형은 페널티에 대한 배치 경사 하강법의 경로이다. 경로는 먼저 W1 =0 에 도달하고 나서 w2 = 0에 다다를 때 까지 좌표축을 따라 내려간다.
오른쪽 위의 그래프에서 등고선이 나타내는 것은 λ = 0.5의 L1 페널티가 더해진 비용함수를 나타낸 것이다. 전역변수 최소값은 w2 축에 있으며, w2 에 도달하고 난 후 전역 최솟값에 도달할 때까지 좁은 경로를 따라 이동하고 있다. 추가적으로 경사 하강법의 경로가 종착지에 근접할 수록 지그재그로 튀는 현상을 볼 수 있는데, 전역 최소값에 수렴하기 위해 학습률을 점진적으로 줄이는 과정에서 갑자기 기울기가 변하기 때문이다. 하단의 2개 그래프 역시 L2 페널티를 이용한 것 외에 동일한 조건이다. 가중치가 완전히 제거 되지 않았지만, 최저값이 규제가 없는 경우 보다 w=0에 더 근접했다.
5. ElasticNet
Ridge 회귀와 LASSO 회귀의 절충안이라고 할 수 있다. 희소한 모델을 만들기 위한 L1 페널티와 선택 특성 개수가 같은 LASSO의 한계를 극복하기 위한 L2 페널티를 가진다. 비용함수는 아래와 같다.
규제항은 Ridge와 Lasso 회귀의 규제항을 단순히 더해서 사용하며 혼합비율 r 을 이용해 조절한다. r = 0 이면 엘라스틱넷은 Ridge 회귀와 같고, r = 1 이면 Lasso 회귀와 같다. 규제가 작게라도 있는 것이 좋기 때문에 일반적으로 평범한 선형회귀는 피해야 한다. 또한 실제로 사용되는 특성이 몇 개뿐인 경우라면, Lasso 나 ElasticNet을 사용하는 것이 좋다. 그리고 특성 수가 훈련 샘플의 수보다 많거나, 특성 몇 개가 과하게 연관되어 있는 경우 Lasso 보다는 ElasticNet을 사용하는 편이 좋다.
'Data Science > 데이터 분석 📊' 카테고리의 다른 글
| [데이터 분석] 13. 최근접 이웃(k Nearest Neighbor) (1) | 2024.08.04 |
|---|---|
| [데이터 분석] 12. 회귀Ⅲ : 로지스틱 회귀 (0) | 2024.08.03 |
| [데이터분석] 10. 회귀Ⅰ: 선형회귀 (0) | 2024.08.01 |
| [데이터 분석] 9. 통계분석Ⅳ: 추정 & 가설검정 - 실습편 (0) | 2024.08.01 |
| [데이터 분석] 8. 통계분석Ⅲ: 추정 & 가설검정 - 이론편 (0) | 2024.07.31 |

1. 규제 (Regularization)
회귀모델에서의 규제란, 부가정보의 손실을 더해 과대적합 문제를 방지하는 방법이며, 복잡도에 대한 페널티를 유도해 모델 파라미터의 값을 감소시킨다. OLS (Ordinary Least Squares, 최소 제곱 회귀)라고 불리는 회귀모델의 일종이며, 과대적합과 부적합 사이의 균형 조정 파라미터로 볼 수 있다. 주로 유전정보나 텍스트 마이닝 같은 입력 파라미터가 너무 많은 문제에 적용되며, 가장 많은 이용방법은 릿지회귀(Ridge) 와 라쏘회귀(Lasso), 엘라스틱넷(ElasticNet)이 있다. 한편, 규제를 적용했을 때 다음과 같은 효과를 볼 수 있다.
규제의 효과
- 모델 트레이닝 속도가 극단적으로 빠르다.
- 변수 중요도 정보를 제공한다.
- 평가가 극단적으로 빠르다.
- 다양한 문제에서 높은 성능을 보인다.
- 선형 모형이 꼭 필요한 경우가 있다.
2. OLS (Ordinary Least Squared)
규제 모델들에 대해 설명하기 앞서, 먼저 회귀모델이 어떤 의미를 갖는지를 생각해보자. 회귀분석의 과정을 생각해보면, 주어진 데이터로부터 X 값들이 주어지고, 그에 대응하는 예측값 y 를 얻을 수 있다. 하지만, 하나의 선으로 모든 y 값을 정확히 나타낼 수 없기 때문에, 실제 결과와 차이는 존재한다. 이 때의 차이를 잔차라고 부르며, 우리가 원하는 것은 이 잔차(ε)가 최소화되는 편향(β)과 각 변수들의 가중치(α)를 찾는 것이 목표라고 볼 수 있다. 이를 수치로 표현하면 다음과 같다.
이를 측정하는 기준 중 하나인 SSE(Sum of Squared Error) 가 있다. 이는 오차의 제곱값을 합한 결과를 의미하는데, 회귀 모델의 목표는 오차가 최소화 되는 값들을 찾는 것이므로 해당 값이 최소화하는 편향과 각 변수들의 가중치를 찾는다고 봐도 무방하다. SSE 를 수식으로 표현하면 다음과 같다.
그리고 지금부터 설명할 OLS는 오차의 제곱을 최소화하는 편향과 각 변수의 가중치를 추정하는 방식이다. 먼저 단순선형회귀 모델에서 어떻게 편향과 변수 가중치를 추정하는지 살펴보자.
위와 같이 편향과 변수의 가중치를 계산할 수 있고, 같은 원리로 다중선형회귀에서도 계산을 해보자.
3. Ridge 회귀 (Ridge Regression)
그렇다면 첫번째 규제로 언급했던, Ridge 회귀(Ridge Regression) 에 대해서 알아보도록 하자. Ridge 회귀는 단순히 최소 제곱 비용 함수에 가중치의 제곱합을 추가한 모델로, 흔히 L2 규제 라고도 부른다. 수식으로 표현하면 다음과 같다.
위의 수식에서 λ||w||22 부분이 규제항(가중치 벡터의 L2 노름)이며 전개해보면 다음과 같다.
하이퍼 파라미터 λ 를 증가시키면 규제 강도가 증가되고 모델의 가중치 값이 감소한다. 만약 λ = 0 일 경우, Ridge 회귀는 선형회귀와 동일하게 된다. 반면 가중치가 아주 큰 경우 모든 가중치가 거의 0에 가까워지고 결국 데이터의 평균을 지나는 수평선이 된다. Ridge 회귀 비용함수에서 절편에 해당하는 w0 는 규제하지 않는다. 모델의 복잡도와 절편은 관계가 없기 때문이다. 만약 경사하강법에 적용하려면 MSE 그레디언트 벡터에 λw 를 더하면 된다. 아래의 그림을 통해 좀 더 살펴보자.

아래의 그래프를 살펴보면 λ 를 증가 시킬 수록 직선에 가까워지는 것을 볼 수 있다.반면 값을 줄이게 되면 모델의 분산은 줄지만 편향이 커지는 현상을 볼 수 있다. 선형 회귀와 마찬가지로 정규방정식을 사용할 수도 있고, 경사하강법을 적용할 수도 있다. 각각의 경우는 아래의 코드로 구현할 수 있다.
import numpy as np
import pandas as pd
from sklearn.linear_model import Ridge, Lasso, ElasticNet, SGDRegressor
from sklearn.model_selection import train_test_split
import statsmodels.api as sm
np.random.seed(42)
data = pd.read_csv("Dataset/housing_data/housing.data.txt", sep="\s+", header=None)
data.columns = ["CRIM", "ZN", "INDUS", "CHAS", "NOX", "RM", "AGE", "DIS", "RAD", "TAX", "PTRATIO", "B", "LSTAT", "MEDV"]
x = data[["LSTAT", "RM", "PTRATIO", "DIS", "NOX", "B", "ZN", "CRIM", "RAD", "TAX"]]
y = data["MEDV"]
# 상수항을 추가합니다.
x = sm.add_constant(x)
# 학습용, 테스트용 데이터 분할
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.3, random_state=42)
# 정규방정식을 적용한 Ridge 회귀
ridge_reg = Ridge(alpha=1, solver="cholesky", random_state=42)
ridge_reg.fit(x_train, y_train)
y_pred = ridge_reg.predict(x_test)library(glmnet)
library(MASS)
# 랜덤 시드 설정
set.seed(42)
# 데이터 읽기
data <- read.table("Data/housing.data.txt", sep="", header=FALSE)
colnames(data) <- c("CRIM", "ZN", "INDUS", "CHAS", "NOX", "RM", "AGE", "DIS", "RAD", "TAX", "PTRATIO", "B", "LSTAT", "MEDV")
# 독립 변수와 종속 변수 분리
x <- data[, c("LSTAT", "RM", "PTRATIO", "DIS", "NOX", "B", "ZN", "CRIM", "RAD", "TAX")]
y <- data$MEDV
# 상수항 추가
x <- cbind(1, x)
# 학습용, 테스트용 데이터 분할
train_indices <- sample(1:nrow(data), size = 0.7 * nrow(data))
x_train <- x[train_indices, ]
y_train <- y[train_indices]
x_test <- x[-train_indices, ]
y_test <- y[-train_indices]
# Ridge 회귀 적용
ridge_reg <- glmnet(as.matrix(x_train), as.matrix(y_train), alpha = 0, lambda = 1)
y_pred <- predict(ridge_reg, newx=as.matrix(x_test))
4. Lasso 회귀 (Lasso Regression)
Lasso 회귀는 Ridge 회귀 처럼 비용 함수에 규제항을 더하지만 L2 노름의 제곱을 2로 나눈 것 대신 가중치 벡터의 L1 노름을 사용한다. 규제 강도에 따라서 어떤 가중치는 0이 될 수 있다. 비용함수는 다음과 같다.
사용된 규제항의 식을 전개하면 아래와 같다.
위의 두 식에 대해 만약 m > n 인 상황이라면 최대 n개의 특성을 선택하는 것이 Lasso 회귀의 한계이다. Lasso 회귀에서의 중요한 특징이 덜 중요한 특성의 가중치를 완전히 제거하려고 하는 것이기 때문이다. 아래 그래프를 통해 좀 더 살펴보자.


위의 그림은 Ridge회귀와 Lasso 회귀를 오차에 적용했을 때의 모습을 보여준다. 우선 왼쪽이 Ridge, 오른쪽이 Lasso 회귀라는 점을 알아두자. 각 그래프에서 중앙에 위치한 원 혹은 마름모 꼴은 페널티를 의미한다. 또한 그래프 우측 상단에 위치한 타원형은 x,y 의 변화량을 β1, β2 라고 할 경우 (β1,β2) 일 때의 자료에 대한 오차집합체라고 할 수 있다. 일반적으로 Lasso 경우 접점에서 만나기 때문에 자료가 넓게 퍼져있는 것을 선호하며, Ridge의 경우 축 위에서 만나기 때문에 가로축의 값이 0이 되는 것을 선호하는 경향을 보인다.
Ridge의 경우, 만약 동심원이 0이 된다(점이 되는 것)이며 타원형이 갖는 오차 범위가 넓어진다. 타원의 중심이면 최적의 값이자 동심원의 최대 크기지만 학습 자료의 데이터이기 때문에 정확한 값은 아니다.(집합체 안의 일부 값들은 스케일 상 너무 큰 값이 있어서 실제사례로는 적합하지않다.) 따라서 두 원의 접점에 있을 때가 더 적합하다. Lasso의 경우 자료오차 차원이 각 축의 점에 걸린다. 즉, 어느 하나만 크게 하고 나머지는 0으로 준다.

이 그림은 각 회귀모델을 배치 경사하강법을 이용해 그래디언트가 이동하는 경로를 표시한 것이다. 왼쪽 위의 그래프 내 배경의 원형 등고선이 규제가 없는 MSE 함수를 의미한다. 마름모 꼴의 등고선은 L1 페널티를 나타내며, 노란색 삼각형은 페널티에 대한 배치 경사 하강법의 경로이다. 경로는 먼저 W1 =0 에 도달하고 나서 w2 = 0에 다다를 때 까지 좌표축을 따라 내려간다.
오른쪽 위의 그래프에서 등고선이 나타내는 것은 λ = 0.5의 L1 페널티가 더해진 비용함수를 나타낸 것이다. 전역변수 최소값은 w2 축에 있으며, w2 에 도달하고 난 후 전역 최솟값에 도달할 때까지 좁은 경로를 따라 이동하고 있다. 추가적으로 경사 하강법의 경로가 종착지에 근접할 수록 지그재그로 튀는 현상을 볼 수 있는데, 전역 최소값에 수렴하기 위해 학습률을 점진적으로 줄이는 과정에서 갑자기 기울기가 변하기 때문이다. 하단의 2개 그래프 역시 L2 페널티를 이용한 것 외에 동일한 조건이다. 가중치가 완전히 제거 되지 않았지만, 최저값이 규제가 없는 경우 보다 w=0에 더 근접했다.
5. ElasticNet
Ridge 회귀와 LASSO 회귀의 절충안이라고 할 수 있다. 희소한 모델을 만들기 위한 L1 페널티와 선택 특성 개수가 같은 LASSO의 한계를 극복하기 위한 L2 페널티를 가진다. 비용함수는 아래와 같다.
규제항은 Ridge와 Lasso 회귀의 규제항을 단순히 더해서 사용하며 혼합비율 r 을 이용해 조절한다. r = 0 이면 엘라스틱넷은 Ridge 회귀와 같고, r = 1 이면 Lasso 회귀와 같다. 규제가 작게라도 있는 것이 좋기 때문에 일반적으로 평범한 선형회귀는 피해야 한다. 또한 실제로 사용되는 특성이 몇 개뿐인 경우라면, Lasso 나 ElasticNet을 사용하는 것이 좋다. 그리고 특성 수가 훈련 샘플의 수보다 많거나, 특성 몇 개가 과하게 연관되어 있는 경우 Lasso 보다는 ElasticNet을 사용하는 편이 좋다.
'Data Science > 데이터 분석 📊' 카테고리의 다른 글
| [데이터 분석] 13. 최근접 이웃(k Nearest Neighbor) (1) | 2024.08.04 |
|---|---|
| [데이터 분석] 12. 회귀Ⅲ : 로지스틱 회귀 (0) | 2024.08.03 |
| [데이터분석] 10. 회귀Ⅰ: 선형회귀 (0) | 2024.08.01 |
| [데이터 분석] 9. 통계분석Ⅳ: 추정 & 가설검정 - 실습편 (0) | 2024.08.01 |
| [데이터 분석] 8. 통계분석Ⅲ: 추정 & 가설검정 - 이론편 (0) | 2024.07.31 |