
1. 최적의 k 값 찾기
비지도학습의 단점은 정답을 모른다는 점이 있다. 데이터 셋에서도 분류문제와 달리 클래스 레이블이 없기 때문에 기존 분류 문제에서 사용했던 성능평가 지표를 사용할 수 없다. 따라서 군집화 모델에 대한 성능평가를 하기 위해서는 알고리즘 자체에서 제공하는 지표를 사용해야만 한다. 앞서 본 K-Means 의 경우, 군집의 성능을 비교하기 위해서는 각 군집 내 SSE(왜곡 혹은 관성)을 사용한다. 또한 파이썬을 사용하는 경우 scikit-learn 의 KMeans() 에서는 모델 학습 시, inertia_ 속성에 계산 및 저장된다.
이처럼 사용해야될 지표가 적고, 모델이 갖는 지표를 활용하게 되므로 결국 최적화를 계산하는 방식으로 성능 평가를 진행해볼 예정이다. 이제부터 다루게 될 2개의 기법은 성능 평가 뿐만 아니라 모델의 최적화까지도 확인할 수 있다는 점을 알아두자.
2. 엘보우 기법
첫 번째로 살펴볼 기법은 엘보우 기법이다. 이 기법은 군집의 SSE를 활용하는 방법으로 그래프를 사용해 문제에 최적인 클러스터의 수를 추정하는 기법이다. 일반적으로 k 값이 증가하게 되면, 군집 내의 왜곡이 감소한다. 이유는 샘플이 할당된 센트로이드에 가까워지기 때문이며, 엘보우 기법은 왜곡이 빠르게 급감하는 지점의 k 값을 찾는다.
이해를 돕기 위해, 아래 예시 코드를 실행해 그래프를 살펴보도록 하자. 예시에서 사용한 모델인 kmeans_plus 는 앞서 K-Means++ 를 설명할 때 사용했던 예시이며, 모델 생성 부분까지는 이전 자료를 참고하면 되기에, 이번 장에서는 생략했다.
...
print('왜곡 : %.2f' % kmeans_plus.inertia_)
distortions = []
for i in range(1, 11):
kmeans_plus = KMeans(n_clusters=i, init='k-means++', n_init=10, max_iter=300, random_state=0)
kmeans_plus.fit(x)
distortions.append(kmeans_plus.inertia_)
plt.plot(range(1, 11), distortions, marker='o')
plt.xlabel('Number of clusters')
plt.ylabel('Distortion')
plt.tight_layout()
plt.show()# 왜곡(distortion) 계산
kmeans_result <- KMeansPP(x, k = 3, nstart = 10)
distortion <- sum(kmeans_result$withinss)
cat(sprintf("왜곡 : %.2f\n", distortion))
# 클러스터 수에 따른 왜곡 계산
distortions <- numeric(10)
for (i in 1:10) {
kmeans_result <- KMeansPP(x, k = i, nstart = 10)
distortions[i] <- sum(kmeans_result$withinss)
}
# 왜곡 그래프 시각화
distortion_data <- data.frame(Clusters = 1:10, Distortion = distortions)
ggplot(distortion_data, aes(x = Clusters, y = Distortion)) +
geom_line() +
geom_point(shape = 1) +
labs(x = "Number of clusters", y = "Distortion") +
theme_minimal()
위의 그래프를 살펴보면, 클러스터 수가 3인 지점에서 그래프의 기울기가 급감하는 것을 볼 수 있다. 이렇듯, 최적의 k 값 이 후 부터는 군집 내 왜곡이 감소한다는 특징을 활용한 기법이며, 만약 알고리즘을 생성했을 때의 k 값과 비교해 모델의 성능도 확인해볼 수 있다.
3. 실루엣 기법
다음으로 알아볼 기법은 실루엣 기법으로, 역시 군집 분석에 대한 평가 기법 중 하나이다. 이 기법은 클러스터 내에 샘플들이 얼마나 조밀하게 모여있는지를 측정하는 그래프 도구이다. 이 때, 각 데이터가 얼마나 조밀하게 모여있는 지를 나타내는 것이 실루엣 계수이며, 해당 기법에서 사용되는 실루엣 계수를 계산하기 위해서는 아래 3단계를 적용하면 된다.
① 샘플 $ {x}^{(i)} $ 와 동일한 클러스터 내 다른 포인트 사이의 거리를 모두 계산한 후, 평균을 내어 클러스터 응집력 $ {a}^{(i)} $ 을 산출한다.
② 샘플 $ {x}^{(i)} $ 와 가장 가까운 클러스터의 모든 샘플간의 평균거리로 최근접 클러스터의 클러스터 분리도 $ {b}^{(i)} $ 를 산출한다.
③ 클러스터 응집력과 분리도 사이의 차이를 둘 중 큰 값으로 나누어 실루엣 계수 $ {S}^{(i)} $ 를 아래 식으로 계산한다.
$ {s}^{(i)} = \frac {{b}^{(i)} - {a}^{(i)} } { max\{{b}^{(i)}, {a}^{(i)}\} } $
실루엣 계수는 일반적으로 -1 ~ 1 사이의 값을 가지며, 위의 수식에서 응집도와 군집도가 같다면, 실루엣 계수는 0이 된다. 반면, 분리도 > 응집력 인 경우에는 실루엣 계수가 1에 가까워지고, 반대로 분리도 < 응집력인 경우에는 -1 에 가까워진다.
결과적으로 클러스터의 분리도란 샘플이 다른 클러스터와 얼마나 다른가를, 클러스터 응집력이란 하나의 클러스터 내에 요소들이 같은 클러스터 내의 다른 요소들과 얼마나 비슷한지를 나타낸다고 할 수 있다. 위의 내용을 코드로 구현하면 아래와 같이 작성할 수 있다.
import numpy as np
from matplotlib import cm
from sklearn.metrics import silhouette_samples
cluster_labels = np.unique(pred_plus)
n_clusters = cluster_labels.shape[0]
silhouette_vals = silhouette_samples(x, pred_plus, metric='euclidean')
y_ax_lower, y_ax_upper = 0, 0
yticks = []
for i, c in enumerate(cluster_labels):
c_silhouette_vals = silhouette_vals[pred_plus == c]
c_silhouette_vals.sort()
y_ax_upper += len(c_silhouette_vals)
color = cm.jet(float(i) / n_clusters)
plt.barh(range(y_ax_lower, y_ax_upper),
c_silhouette_vals,
height=1.0,
edgecolor='none',
color=color)
yticks.append((y_ax_upper + y_ax_lower) / 2.)
y_ax_lower += len(c_silhouette_vals)
silhouette_avg = np.mean(c_silhouette_vals)
plt.axvline(silhouette_avg, color='red', linestyle='--')
plt.yticks(yticks, cluster_labels + 1)
plt.ylabel('Cluster')
plt.xlabel('Silhouette Coefficient')
plt.tight_layout()
plt.show()# 필요한 라이브러리 로드
library(cluster) # silhouette() 함수 사용
library(ggplot2) # 시각화
library(RColorBrewer)
# 클러스터 예측 결과는 pred_plus로 가정 (이전에 KMeansPP를 통해 생성됨)
# 실루엣 값 계산
silhouette_vals <- silhouette(pred_plus, dist(x, method = "euclidean"))
# 클러스터 라벨
cluster_labels <- unique(pred_plus)
n_clusters <- length(cluster_labels)
# 실루엣 값 시각화를 위한 데이터 준비
silhouette_df <- data.frame(
cluster = factor(silhouette_vals[, 1]),
silhouette_width = silhouette_vals[, 3],
sample_order = 1:nrow(silhouette_vals)
)
# 실루엣 값을 클러스터별로 정렬
silhouette_df <- silhouette_df[order(silhouette_df$cluster, silhouette_df$silhouette_width), ]
# 클러스터별로 막대 그래프 그리기
ggplot(silhouette_df, aes(x = sample_order, y = silhouette_width, fill = cluster)) +
geom_bar(stat = "identity", width = 1) +
scale_fill_brewer(palette = "Set3") +
geom_vline(xintercept = mean(silhouette_vals[, 3]), color = "red", linetype = "dashed") +
labs(x = "Sample Index", y = "Silhouette Coefficient", title = "Silhouette Plot") +
theme_minimal() +
theme(legend.position = "bottom")
위의 그래프를 통해서 알 수 있듯이, 3개의 군집 모두 1에 가까운 실루엣 계수를 갖는 것으로 보아 군집이 잘 형성됬다고 볼 수 있다. 만약 군집화가 잘못된다면 어떤 형태일지 살펴보기 위해, k=2로 설정하고 같은 코드를 수행하게되면 아래의 결과와 유사한 형태로 나타날 것이다.
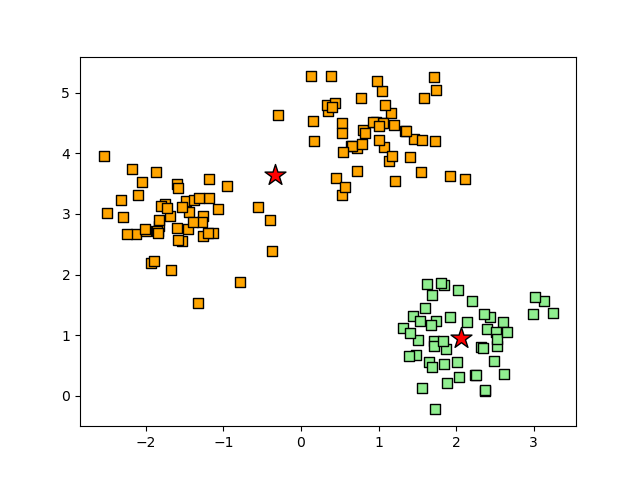

산점도에서 2번 군집의 중심이 두 군집 사이엥 위치한다고 예측했으며, 실루엣 그래프의 경우도 길아나 두께가 서로 확실히 다르다는 것이 확인된다.
'Data Science > 데이터 분석 📊' 카테고리의 다른 글
| [데이터 분석] 24. SOM (Self-Organizing Map) (0) | 2024.10.13 |
|---|---|
| [데이터 분석] 22. 클러스터링 Ⅱ : 계층적 군집 (0) | 2024.10.11 |
| [데이터 분석] 21. 클러스터링 Ⅰ : K-Means (0) | 2024.10.09 |
| [데이터 분석] 20. 차원 축소 (Dimensional Reduction) Ⅱ : 커널 PCA, LLE, LDA (0) | 2024.10.07 |
| [데이터 분석] 19. 차원 축소 (Dimensional Reduction) Ⅰ : PCA (0) | 2024.09.29 |