[데이터 분석] 21. 클러스터링 Ⅰ : K-Means

1. 클러스터링?

이전까지 회귀나 분류는 정답이 존재하는, 정확히는 반응변수(혹은 결과변수)가 존재하는 지도학습의 과정이였다면, 클러스터링은 비지도학습에 해당하는 대표적인 기법으로 학습 데이터 내에 레이블(label)이 존재하지 않다는 특징이 있다. 
비지도학습의 장점은 데이터 셋 내에 사용자도 모르는 숨겨진 구조를 찾아낼 수 있다는 점이다. 이제부터 다뤄볼 클러스터링은 데이터를 각각의 군집으로 묶어서, 같은 군집의 요소들은 서로 비슷하게, 다른 군집에 속한 요소들과는 최대한 다르도록 하여 자연스러운 그룹을 찾는 기법이라고 할 수 있다. 

1.1 군집화

모델들을 소개하기에 앞서 군집화에 대한 정의를 이해할 필요가 있다. 군집이란 비슷한 객체로 이루어진 그룹을 찾는 기법이며, 앞서 설명한 것처럼, 한 그룹 안의 객체들은 다른 그룹에 있는 객체보다 더 관련이 많다. 대표적인 예시로 문서, 음악, 영화를 여러 주제의 그룹으로 모으는 경우가 있다. 

군집화의 종류에는 크게 프로토타입 기반, 계층적 군집, 밀집도 기반 군집으로 나눠볼 수 있으며, 이번 장에서 다룰 K-Means 알고리즘의 경우 프로토타입 기반의 군집화에 속한다. 

 

2. K-Means

이번 장에서 다루게 될 K-Means 알고리즘은 대표적인 클러스터링 기법이라고 할 수 있다. 또한 위에서 언급한 것처럼 군집화 종류 중에서는 프로토타입 기반의 군집화에 해당하는데, 각 클러스터가 하나의 프로토 타입으로 표현되며, 연속적인 특성에서는 비슷한 데이터 포인트가 평균으로, 범주형 특성에서는 가장 대표가 되는 포인트가 된다.
해당 알고리즘에서 가장 중요한 것은 군집의 개수를 의미하는 K 값을 적절히 설정해야한다는 것인데, 이 후에 모델 성능 평가부분에서 다루게 될 엘보우 기법이나 실루엣 기법을 이용해서 적절한 K 값을 찾을 수 있다.

그렇다면 K-Means 알고리즘이 어떻게 동작하는 지를 살펴보도록 하자. 알고리즘의 과정은 크게 아래와 같이 4단계로 나타낼 수 있으며, 적절한 K 값을 찾을 때까지 반복한다.

① 샘플 포인트에서 랜덤하게 k개의 평균 값을 초기 클러스터 중심으로 선택한다.
② 각 샘플을 가장 가까운 평균 값 $ {\mu}^{(j)} , j \in {{l, ..., k}} $ 에 할당한다.
③ 할당된 샘플들의 중심으로 평균을 이동한다.
④ 클러스터 할당이 변함 없거나, 사용자가 지정한 허용오차 또는 최대 반복횟수에 도달할 때까지 ②, ③ 과정을 반복한다.

이 때, 샘플 간의 유사도는 거리의 반대 개념으로, 일반적인 경우 m차원 공간에 있는 두 포인트의 유클리디안 거리의 제곱으로 계산된다. 구체적인 수식은 아래와 같다. 

 

$ {d(x, y)}^{2} = \sum_{j=1}^{m} {{x}_{j} - {y}_{j}}^{2} = {\Vert x-y \Vert}_{2}^{2} $

 

위의 식을 기반으로 클러스터 내 제곱 오차합은 아래와 같이 계산하게 된다. 

 

$ SSE = \sum_{i=1}^{n} \sum_{j=1}^{m} {w}^{(i, j)} = {\Vert {x}^{(i)} - {\mu}^{(j)} \Vert}_{2}^{2} $

 

위의 식에서 $\mu$ 는 클러스터의 대표 포인트(센트로이드, Centroid) 를 의미한다. 만약 샘플 x 가 클러스터 j 내에 존재한다면, $ {w}^{(i, j)} $ 는 1이 되고, 아니면 0이 된다. 

다음으로 K-Means 알고리즘의 사용법을 살펴보도록 하자. Python 및 R에서 사용 방법은 아래 코드와 같으니 사용 언어에 맞게 참고하기 바란다. 

from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs

from matplotlib import pyplot as plt

x, y = make_blobs(n_samples=150, n_features=2, centers=3, cluster_std=0.5, shuffle=True, random_state=0)

plt.scatter(x[:, 0], x[:, 1], c='white', marker='o', edgecolors='black', s=50)
plt.grid()
plt.tight_layout()
plt.show()

kmeans = KMeans(
	n_clusters=3,  # 클러스터 수 
	init='random', # 초기값 설정
 	n_init=10,     # 초기 포인트 수
 	max_iter=300,  # 최대 반복 횟수
	tol=1e-04,     # 사용자 지정 허용 오차
	random_state=0 # 난수 생성
)

y_pred = kmeans.fit_predict(x)

결과로 산출된 군집을 확인해보면 아래 그래프와 같이 나오게 된다. 

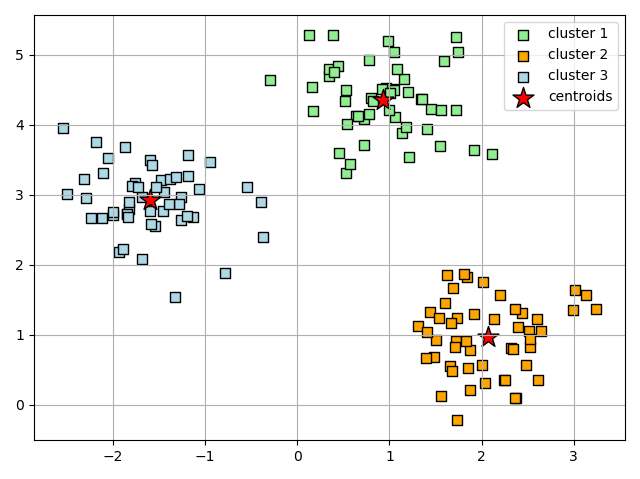
위의 산점도에서 K-Means 알고리즘이 원형 중심부에 3개의 센트로이드를 할당한 것을 확인할 수 있다. 보통 작은 데이터 셋에서는 잘 동작하지만, 사전에 군집의 개수인 k 를 잘 설정해줘야만 동작한다는 단점이 있다. 

3. K-Means ++

추가적으로 K-Means 와 관련된 알고리즘을 알아보도록 하자. 앞서 살펴본 K-Means 알고리즘의 경우, 초기 센트로이드 값을 랜덤하게 설정하기 때문에 초기 값이 나쁠 경우 군집 결과까지 나쁜 군집으로 만들 수 있다. 이를 개선하기 위해서 고안된 알고리즘이 지금 소개할 K-Means++ 알고리즘이다. K-Means 와의 차이점으로는 초기 센트로이드가 서로 떨어지지 않도록 위치시킨 후 K-Means 군집화가 진행된다. 자세한 알고리즘 과정은 아래와 같다.

① 선택한 k 개의 센트로이드를 저장할 빈 집합 M을 초기화한다. 
② 입력 샘플에서 첫 번째 센트로이드 $ {\mu}^{(i)} $ 를 랜덤하게 선택하고 M에 할당한다.
③ M에 있지 않은 각 샘플 $ {x}^{(i)} $ 에 대해 M에 있는 센트로이드까지 최소 제곱 거리를 찾는다.
④ 아래 식과 같은 가중치가 적용된 확률분포를 사용하여 센트로이드 $ {\mu}^{(i)} $ 를 랜덤하게 선택한다. 

$ \frac { { d({\mu}^{(p)}, M) }^{2} } { \sum_{i} {d({x}^{2}, M)}^{2} } $

⑤ k 개의 센트로이드가 나올 때까지 ② 와 ③을 반복한다.
⑥ 이 후 K-Means 를 수행한다.

위의 과정을 알고리즘으로 구현하면 다음과 같다. 추가적으로 파이썬의 경우, scikit-learn 의 K-Means 클래스로 K-Means++ 를 구현하기 위해서는 init 매개변수에 "k-means++" 로 설정하면 된다. 구체적인 코드는 다음과 같다.

kmeans_plus = KMeans(n_clusters=3, init="k-means++", n_init=10, max_iter=300, tol=1e-04, random_state=0)
pred_plus = kmeans_plus.fit_predict(x)

library(TreeDist)

set.seed(0)  # 파이썬의 random_state와 동일하게 설정
kmeans_result <- KMeansPP(x, k = 3, nstart = 10)

pred_plus <- kmeans_result$cluster
print(pred_plus)