[데이터 분석] 8. 통계분석Ⅲ: 추정 & 가설검정 - 이론편

1. 추정

가설검정에 대해 설명하기 앞서, 먼저 가설을 세우기 위한 기초단계를 먼저 알아보도록 하자. 바로 추정이라는 것인데, 추정에 대한 사전적인 의미는 "입력된 자료가 불완전하거나 불확실하더라도 사용할 수 있는 계산 결과의 근삿값" 을 의미한다. 이를 통계에서는 "모집단을 대표할 수 있는 일부를 표본으로 추출하여 분석한 통계량을 통해 모집단의 특징(모수)을 예측하는 과정"이라고 할 수 있다. 이렇게 통계량을 통해 모집단의 특징을 예측하는 과정을 통계적 추론이라고 하며, 대표적으로 추정과 가설검정이 있다. 추정은 모수를 어떤 값으로 정의하는가에 따라 크게 점추정과 구간추정으로 나눌 수 있다. 점추정은 "모수들 중에 가장 알맞는(참인) 값이라 여겨지는 하나의 모수를 선택하는 것"이다. 쉽게 말해서, 모수를 하나의 값으로 표시하는 것을 의미한다.

반대로 구간추정은 "모수를 특정 값으로 지정하기에 정확하지 않기 때문에 범위를 넓혀 구간으로 모수를 선택하는 것"을 의미한다. 앞서 말한 점추정의 경우, 1개 값으로 표현되며, 통계적으로 모수를 표현하기에 정확도가 낮다는 단점이 있다. 이를 보완하기 위해서 점이 아닌 특정 구간에 모수가 존재한다고 범위를 넓혀 정확도를 높이기 위한 추정 방법이라고 볼 수 있다. 때문에 일정크기의 신뢰수준으로 모수가 특정 구간에 존재할 것이라 선언한다고도 볼 수 있다.

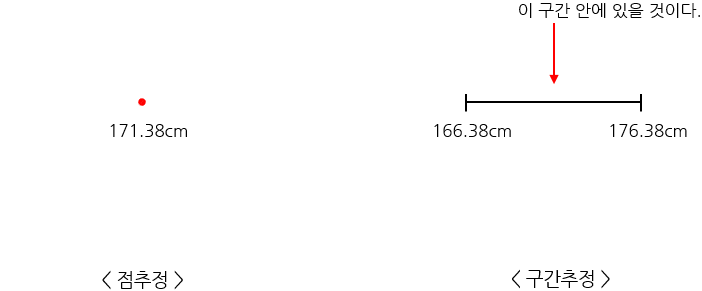
값의 범위를 구하는 절차에서 미지의 모수가 위치할 범위를 의미하기 때문에 신뢰구간이라고도 부른다. 정확히는 정해진 신뢰수준(1-α)에 따라 실제 모수가 있을 것이라 예상하는 구간이라고 할 수 있으며, 일반적으로 90%, 95%, 99%의 확률을 이용한다.

2. 가설검정

다음으로 가설검정에 대해 알아보자. 앞서 본 추정과 같이 통계적 추론 방식 중 하나이며, 모집단에 대한 가설(귀무가설)을 설정한 후, 모집단에 대한 가설이 옳다는 전제하에 표본 관찰을 통해 관측된 통계량(검정통계량) 보다 증명하고자 하는 가설(대립가설)을 지지하는 값이 나타날 확률을 구하여 모집단에 대한 가설의 채택여부를 결정하는 분석법이다. 이 때 검정하고자 하는 모집단의 모수를 기본 설정으로 한다. 그리고 이를 통해 해당 자료가 특정 추정이나 가설과 양립하는 지도 확인이 가능하다. 한 편, 가설검정에서는 주요 개념이 몇 개 있는데 아래에서 하나씩 살펴보도록 하자.

2.1 귀무가설 vs. 대립가설

가설검정을 할 때는 귀무가설과 이와 반대되는 대립가설을 설정해야한다. 먼저 귀무가설이란, 일반적인 사실로 받아들여지는 가설을 의미한다. 이는 표본관찰을 통해 사실이 아니라고 확신하기 전까지 사실이라고 채택되는 가설이므로 가설검정을 시작할 때는 귀무가설이 옳다는 전제 하에 진행된다. 표시는 H0 로 표시한다. 반대로 대립가설은 우리가 표본관찰을 통해 확실하게 증명하고 싶은 가설로 뚜렷한 증거가 있어야 채택할 수 있는 가설을 의미한다. 이는 연구자가 새로이 주장하여 검정하고자 하는 연구가설이기에 앞서 언급했듯이, 귀무가설을 기각할 수 있는 논리적인 근거가 존재해야한다. 표시는 H1으로 표시한다.

2.2 검정통계량

그렇다면 귀무가설과 대립가설 중 어떤 가설이 맞는지에 대한 판단은 어떻게 할까? 여러 지표들을 사용하지만, 그 중 하나로 검정통계량을 사용한다. 검정통계량은 표본으로부터 추출한 통계량이나 검정에 사용할 분포에 따라 그에 맞는 값으로 치환한 통계량이며, 검정통계량의 값을 토대로 귀무가설을 기각할지에 대한 여부를 결정한다. 만약 귀무가설이 참이라면, 확률분포가 완전하게 알려지고, 귀무가설이 참이 아닐 경우 다른 분포를 갖는다.

$$t=\frac{{b}_k-{\beta }_k}{se({b}_k)}-t(N-2)$$

2.3 가설 검정의 오류

귀무가설와 대립가설의 채택여부에 대한 판단지표 중 다른 하나는 P-Value 를 확인하는 것이다. P-value 란 귀무가설이 사실일 때 관측된 검정통계량의 값보다 귀무가설에 대해 예외적인 상황이 나올 확률의 크기를 의미한다. 이를 이해하기 위해서는 먼저 가설검정의 오류에 대해서 살펴봐야한다.

가설 검정의 오류란, 앞서 귀무가설과 대립가설 중 어떤 가설을 채택할 지를 결정하는 과정을 수행하는데, 이 때 발생하는 오류를 의미하며, 제 1종 오류와 제 2종 오류가 있다. 먼저 제 1종 오류는 귀무가설이 옳음에도 기각을 하는 경우를 의미하며, 제 2 종 오류는 귀무가설이 옳지 않아도 채택하는 경우를 의미한다.

이 중 제 1종 오류를 범할 확률의 최대 범위(최대허용오차)를 가리켜 유의수준이라고 부른다. 일반적으로 유의수준은 0.01, 0.05, 0.1 중에서 설정하며, 만약 검정통계량이 유의수준보다 작은 값이 나온다면, 귀무가설이 채택될 가능성이 적다고 해석할 수 있다. 또한 귀무가설이 옳다는 전제 하에 관측된 검정통계량의 분포에서 확률이 유의수준이라면, 이를 가리켜 기각역이라고 하며, 앞서 P-value 가 귀무가설이 참인 상황에서 예외적인 상황이 나타날 확률을 가리키며, 만약 그 값이 유의수준보다 적은 값이 나오게 되면, 귀무가설이 채택될 가능성이 낮아지기 때문에 채택여부를 판단하는 지표로 사용되는 것이다.

그렇다면 실제 가설검정을 어떻게 수행하는지 다음 장에서 실습을 통해 살펴보도록 하자.